Das Vektorprodukt
Das Vektorprodukt, auch Kreuzprodukt genannt, ist häufig hilfreich,
wenn man einen Normalenvektor ermitteln soll, um eine Ebenengleichung aufzustellen,
oder um die Darstellungsform einer Ebene in eine andere umzuwandeln.
Verwechseln Sie das Vektorprodukt nicht mit dem Skalarprodukt!
Sie können sich den Unterschied ggf. so merken: Beim Skalarprodukt kommt eine Zahl (ein Skalar)
heraus, beim Vektorprodukt ein Vektor.
Das Vektorprodukt ist wie folgt definiert:
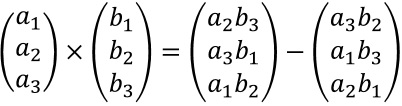
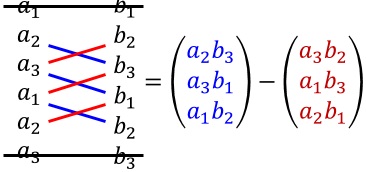
- Schreibe die Vektoren zweimal untereinander und streiche die obere und untere Zeile.
- Bilde Produkte entlang der blauen und roten Linien und berechne "blaue Produkte minus rote Produkte". Sie können sich das ggf. auch in der Form "absteigende Produkte minus aufsteigende Produkte" merken.
Eigenschaften des Vektorprodukts
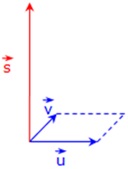
Die für uns wichtige Eigenschaft des Vektorprodukts besteht darin, dass der Ergebnisvektor senkrecht auf den beiden ursprünglichen Vektoren steht! Somit können Sie zu zwei gegebenen Vektoren mit Hilfe des Vektorprodukts immer einen Normalenvektor finden.
Die zweite bemerkenswerte Eigenschaft besteht darin, dass die Länge des Ergebnisvektors genau dem Flächeninhalt des Parallelogramms entspricht, das von den ursprünglichen beiden Vektoren "aufgespannt" wird!
Rechenbeispiel 1
Bestimme das Kreuzprodukt der beiden Vektoren
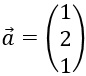 und
und 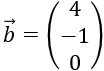 .
.Lösung
Wir gehen nach dem "Schnürsenkelverfahren" vor und berechnen "absteigende Produkte minus aufsteigende Produkte".
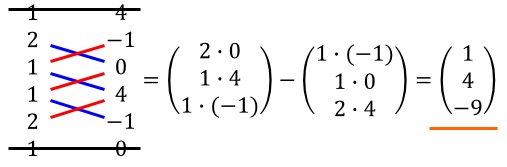
Rechenbeispiel 2
Gegeben sei die Ebene E mit
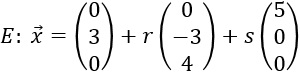 .
.Bestimme einen Normalenvektor zu E.
Lösung
Bilde das Vektorprodukt der beiden Richtungsvektoren:
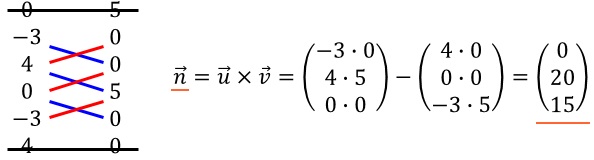
Einen Normalenvektor bestimmen
Wir haben nun gesehen, wie man mit dem Vektorprodukt einen Normalenvektor senkrecht zu zwei gegebenen Vektoren bestimmen kann. Es gibt aber noch einen weiteren Weg! Wenn
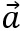 und
und 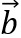 gegeben sind, und
gegeben sind, und 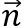 senkrecht zu beiden Vektoren stehen soll, so muss sowohl
senkrecht zu beiden Vektoren stehen soll, so muss sowohl
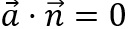 als auch
als auch
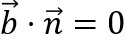 gelten.
Daraus ergibt sich ein lineares Gleichungssystem, aus dem sich
gelten.
Daraus ergibt sich ein lineares Gleichungssystem, aus dem sich
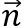 bestimmen lässt.
Wir zeigen dies an einem Rechenbeispiel.
bestimmen lässt.
Wir zeigen dies an einem Rechenbeispiel.Rechenbeispiel
Es seien
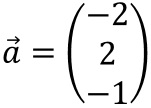 und
und
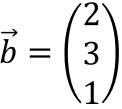 .
.Gesucht ist ein Vektor
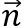 ,
der sowohl senkrecht auf
,
der sowohl senkrecht auf 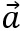 als
auch senkrecht auf
als
auch senkrecht auf 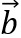 steht.
steht.Lösung
Es sei
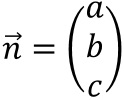 .
.Damit folgt
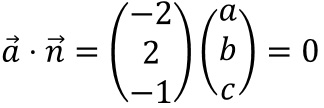 und
und
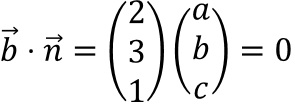 .
.Daraus ergibt sich das folgende LGS:
I. -2a+2b-c=0 und II. 2a+3b+c=0
Das LGS hat mehr Variablen als Gleichungen, d.h. wir können eine der Variablen, sagen wir c, frei wählen. Für c wählen wir einen möglichst einfachen Wert, aber nicht c=0, denn dann wären auch a=0 und b=0, was uns jedenfalls nicht zu einem von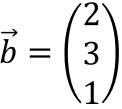 verschiedenen Normalenvektor führt. Daher wählen wir z.B. c=1.
Jetzt haben wir
verschiedenen Normalenvektor führt. Daher wählen wir z.B. c=1.
Jetzt haben wir
I. -2a+2b-1=0 und II. 2b+3b+1=0.
Es folgt I. -2a+2b=1 und II. 2a+3b=-1.Addition der beiden Gleichungen liefert 5b=0 also b=0.
Eingesetzt in II. liefert dies a=-1/2.
Schließlich haben wir mit
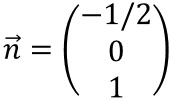 einen Normalenvektor gefunden, der senkrecht zu
einen Normalenvektor gefunden, der senkrecht zu
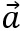 und
und
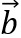 steht.
steht.Bemerkung
Ob Sie nun einen Normalenvektor mit Hilfe des Vektorprodukts oder mit dem Skalarprodukt und anschließendem Lösen eines LGS bestimmen, bleibt natürlich Ihnen überlassen. Das ist wohl eine reine Geschmacksfrage. Beide Lösungswege sind ähnlich aufwändig!
| Downloads |
PowerPoint